hello
since we're given y and x intercept, we can use it to find the slope of the equation
y-intercept = 2.1
x-intercept = 3.5
what this implies that in a given graph, y-axis is (0, 2.1) and x-axis (3.5, 0)
now we can use this co-ordinate to find our slope
so our odered pair are (3.5, 0) and (0, 2.1)
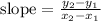
y2 = 2.1
y1 = 0
x2 = 0
x 1 = 3.5
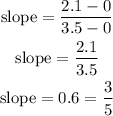
now we know our slope as 3/5
we can use this slope to find the equation of the line
remember our y-intercept = 2.1
equation of staright line is given as y = mx + c
m = slope
c = y-intercept
now, the equation of this line is
y = 3/5x + 2.1
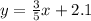
b.
we have one point (1.2, 5.1) and an x-intercept of 3.7
let the first point (1.2, 5.1) be A and the second point as B
A = (1.2, 5.1)
B = (3.7, 0)
y2 = 0
x2 = 3.7
y1 = 5.1
x1 = 1.2
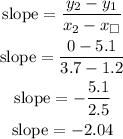
y = mx + c
m = slope
c = y-intercept
let's use co-ordinate B to find our y-intercept
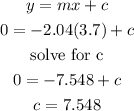
we can now re-write our equation with the standard form of y = mx + c
y = -2.04x + 7.548