Question

Find the vertex by using the vertex formula. Express numbers in simplest form.m(x)=x^2-4x+11 can you help me with this

Answer 1

Answer;

`\text{Vertex = (2,7)}`

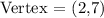
Explanation;

Here, we want to get the vertex of the given quadratic equation

We have the vertex form as;

`m(x)=a(x-h)^2+k`

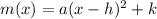
where the vertex is;

`(h,k)`

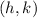
The parameters of the parabola represents the coefficient of each individual unit

The coefficient of x^2 is 1

The coefficient of x is -4

The coefficient of the last number is 11

Now, we get the value of h as follows;

`h\text{ = }(-b)/(2a)\text{ =}(4)/(2)\text{ = 2}`

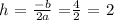
To get the value of k, we susbtitute the value of h for x

So, we have;

`\begin{gathered} m(2)=2^2-4(2)+11 \\ m(2)=7 \end{gathered}`

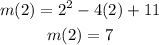
So, we have the value of k as 7

The vertex is thus a minimum at (2,7)