Question

The ratio of the sides of two similar squares is 2:3. If the area of the larger square is 225 square units, find the area of the smaller square.

Answer 1

To answer this question, we need to know that if we have that two figures are similar, then their corresponding sides are proportional - they have the same ratio. If we have, as in this case, the area, we need to square the ratio of the corresponding sides.

Then, if we have that the ratio of the sides of two similar squares is 2 : 3, then the ratio between their areas is the square of this ratio as follows:

Now, we have that the area of the larger square is 225 square units. Then, we have that the area of the smaller square is:

`(A_(smaller))/(A_(larger))=(4)/(9)_{}\Rightarrow A_(smaller)=225\cdot(4)/(9)\Rightarrow A_(smaller)=100sq.units`

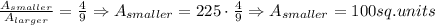
In summary, therefore, the area of the smaller square is equal to 100 square units.