Given the following recursive rule:
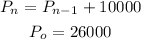
We will find the following:
(a) Calculate P₁ and P₂
so, the value of P₁ = 26000
and P₂ = P₁ + 10000 = 26000 + 10000 = 36000
P₂ = 36000
(b) Find an explicit formula for Pn
so,
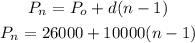
(c) Use the explicit formula to predict the store's sales in 10 years.
so, substitute with n = 10
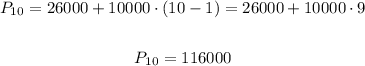
(d) When will the store's sales exceed $139,000?
so, we will substitute with Pn = 139000, then solve the equation to find (n)
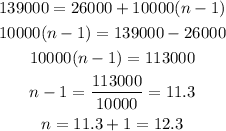
So, the answer will be after 12.3 years