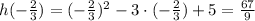Question

3) Use f(x) = -2x2 - 4 and h(x) = x2 - 3x + 5 to answer questions

Answer 1

Given the functions :

`\begin{gathered} f(x)=-2x^2-4 \\ h(x)=x^2-3x+5 \end{gathered}`

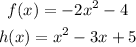
a. find f ( -1/4)

so, substitute with x = -1/4 at the function f

`f(-(1)/(4))=-2\cdot(-(1)/(4))^2-4=-2\cdot(1)/(16)-4=-(1)/(8)-4=-4.125`

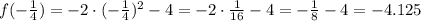
b. find f(-3x+2)

so, substitute with x = -3x + 2

`\begin{gathered} f(-3x+2)=-2\cdot(-3x+2)^2-4 \\ =-2\cdot(9x^2-12x+4)-4 \\ =-18x^2+24x-8+4 \\ =-18x^2+24x-4 \end{gathered}`

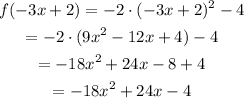
C. find h (5x) - 4

So, the answer will be :

`\begin{gathered} h(5x)-4=(5x)^2-3\cdot(5x)+5-4 \\ \end{gathered}`

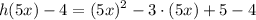
d. -4h(3+k)

so, the answer will be :

`-4h(3+k)=-4\cdot\lbrack(3+k)^2-3\cdot(3+k)+5\rbrack`

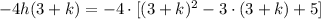
e. f(-x^3)

So ,the answer will be :

`\begin{gathered} f(-x)^3=-2\cdot(-x^3)^2-4 \\ \end{gathered}`

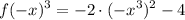
f. h(-2/3)

So, the answer will be :

`h(-(2)/(3))=(-(2)/(3))^2-3\cdot(-(2)/(3))+5=(67)/(9)`