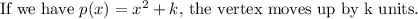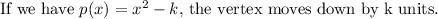Given:
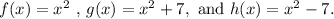
Required:
We need to graph the given functions.
Step-by-step explanation:

The given equation is the parabola equation.
The leading cod\efficient of the given function is 1 which is greater than zero.
We know that If the leading coefficient is greater than zero, the parabola opens upward.
f(x) is an open upward parabola.
The function f(x) is of the form

where a=1, h=0 and k=0.
The vertex (h,k) =(0,0).
Set x =1 and substitute in the function f(x) to find the point lying on the parabola.


We get the point (1,1).
Draw an open upward parabola with vertex (0,0) and through the point (1,1).
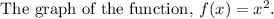
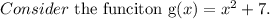
g(x) is an open upward parabola since the leading coefficient is greater than zero.
The function g(x) is of the form

where a=1, h=0 and k=7.
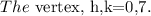
Set x =1 and substitute in the function g(x) to find the point lying on the parabola.

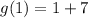

We ge the point (1,8).
Draw an open upward parabola with vertex (0,7) and through the point (1,8).
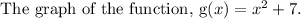
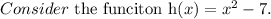
h(x) is an open upward parabola since the leading coefficient is greater than zero.
The function h(x) is of the form

where a=1, h=0 and k=-7.
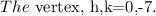
Set x =1 and substitute in the function h(x) to find the point lying on the parabola.

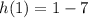

We ge the point (1,-6).
Draw an open upward parabola with vertex (0,-7) and through the point (1,-6).
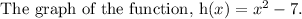

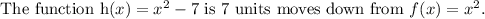
Final answer: