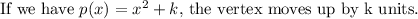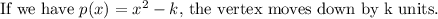Question

Graph the functions f ( x ) = x^2 , g ( x ) = x^2 + 7 , and h ( x ) = x^2 − 7 on the same rectangular coordinate system. Then describe what effect adding a constant, k , to the function has on the vertex of the basic parabola.

Answer 1

Given:

`f(x)=x^2\text{ , }g(x)=x^2+7,\text{ and }h(x)=x^2-7.`

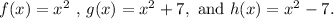
Required:

We need to graph the given functions.

Step-by-step explanation:

`Consider\text{ the funciton}f(x)=x^2.`

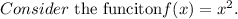
The given equation is the parabola equation.

The leading cod\efficient of the given function is 1 which is greater than zero.

We know that If the leading coefficient is greater than zero, the parabola opens upward.

f(x) is an open upward parabola.

The function f(x) is of the form

`y=a(x-h)^2+k`

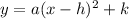
where a=1, h=0 and k=0.

The vertex (h,k) =(0,0).

Set x =1 and substitute in the function f(x) to find the point lying on the parabola.

`f(1)=(1)^2`
`f(1)=1`

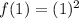
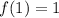
We get the point (1,1).

Draw an open upward parabola with vertex (0,0) and through the point (1,1).

`\text{ The graph of the function, }f(x)=x^2.`

`Consider\text{ the funciton g}(x)=x^2+7.`

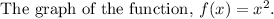
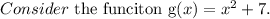
g(x) is an open upward parabola since the leading coefficient is greater than zero.

The function g(x) is of the form

`y=a(x-h)^2+k`

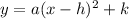
where a=1, h=0 and k=7.

`The\text{ vertex, \lparen h,k\rparen=\lparen0,7\rparen.}`

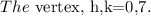
Set x =1 and substitute in the function g(x) to find the point lying on the parabola.

`g(1)=(1)^2+7`

`g(1)=1+7`
`g(1)=8`

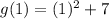
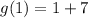
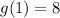
We ge the point (1,8).

Draw an open upward parabola with vertex (0,7) and through the point (1,8).

`\text{ The graph of the function, g}(x)=x^2+7.`

`Consider\text{ the funciton h}(x)=x^2-7.`

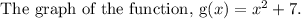
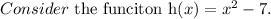
h(x) is an open upward parabola since the leading coefficient is greater than zero.

The function h(x) is of the form

`y=a(x-h)^2+k`

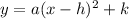
where a=1, h=0 and k=-7.

`The\text{ vertex, \lparen h,k\rparen=\lparen0,-7\rparen.}`

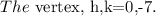
Set x =1 and substitute in the function h(x) to find the point lying on the parabola.

`h(1)=(1)^2-7`

`h(1)=1-7`
`h(1)=-6`

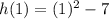
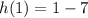
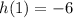
We ge the point (1,-6).

Draw an open upward parabola with vertex (0,-7) and through the point (1,-6).

`\text{ The graph of the function, h}(x)=x^2-7.`

`\text{ The function }g(x)=x^2+7\text{ is 7 units moves up from }f(x)=x^2.\text{ }`

`\text{ The function h}(x)=x^2-7\text{ is 7 units moves down from }f(x)=x^2.\text{ }`

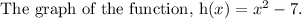
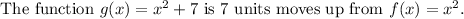
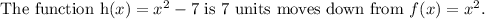
Final answer:

`\text{If we have }p(x)=x^2+k\text{, the vertex moves up by k units.}`

`\text{If we have }p(x)=x^2-k\text{, the vertex moves down by k units.}`