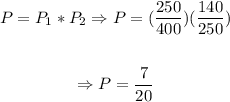Question

A cell phone company gets a really good deal on 400 Samsung phones. Of them, 250 have 5’ screens, 140 are silver and the rest are black. Of the phones with 4” screens, 80 are silver and the rest are black. If one phone is picked at a random for a customer, find the probability that it will Be silver or have a 5” screen.Answer will be a fraction

Answer 1

We will have that the probability of it will be the probability that the phone is silver under the conditionality of it being a 5" screen, that is:

`\begin{gathered} P=(250)/(400)\ast(140)/(250)\Rightarrow P=(7)/(20) \\ \\ \end{gathered}`

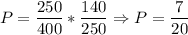
So, the probability will be 7/20.

***Explanation***

First, we know that the probability of one event happening one after another is the product of those probabilities.

Now, first, we can see that the probability of the phone being a 5" screen is given by the number of 5" screen phones over the total number of phones, from the data that probability 250 5" screen phones over a total of 400 phones:

`P_1=(250)/(400)`

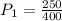
Then, we determine the probability of those 5" phones to be silver. We know that there are 140 5" silver phones and the total of 5" phones is 250, so the probability of this is:

`P_2=(140)/(250)`

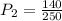
Finally, since the total probability is the product of those probabilities, we will have that:

`\begin{gathered} P=P_1\ast P_2\Rightarrow P=((250)/(400))((140)/(250)) \\ \\ \Rightarrow P=(7)/(20) \end{gathered}`