Step-by-step explanation:
The expression that we have is
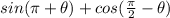
And we need to simplify and find the result.
Step 1. First, we use the following property of the sine to simplify the first term
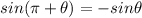
Therefore, the expression now is:
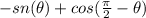
Step 2. Then we use the following cosine property to simplify the second term:
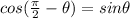
Substituting this into our expression:
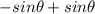
Step 3. We have the same expression sine of theta with negative and positive signs and they cancel each other. The result is 0:
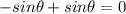
Answer: 0