Question

Find the vertical and Horizontal asymptotes, Holes, Domain, RangeAlso grapgh it

Answer 1

We have the expression:

`y=(x+2)/(x^2+5x+6)`

We will start factorizing the denominator:

`\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4\cdot1\cdot6}}{2} \\ x=\frac{-5\pm\sqrt[]{25-24}}{2} \\ x=\frac{-5\pm\sqrt[]{1}}{2} \\ x=(-5\pm1)/(2) \\ x_1=(-5-1)/(2)=-(6)/(2)=-3 \\ x_2=(-5+1)/(2)=-(4)/(2)=-2 \\ \Rightarrow x^2+5x+6=(x+3)(x+2) \end{gathered}`

Then, we can simplify the expression as:

`y=(x+2)/(x^2+5x+6)=(x+2)/((x+3)(x+2))=(1)/(x+3)`

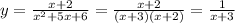
We will have a vertical assymptote at the discontinuity x=-3:

`\begin{gathered} \lim _(x\to-3+)y=\infty \\ \lim _(x\to-3-)y=-\infty \end{gathered}`

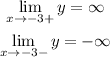
As holes, we can consider x=-2, because in the original equation it would make a discontinuity (it would make zero the quadratic denominator and the numerator), but not an assymptote. The limit exists but the function is not defined for x=-2.

Then, as x=-3 and x=-2 are discontinuities, the domain is D: x in R .

We can calculate if there is an horizontal assymptote calculating the limit of y when x approaches infinity:

`\lim _(x\to\infty)(1)/(x+3)=0`

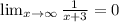
Then, as 0 is a finite value, we have an HA at y=0.

The range is all the values that y can take given the domain.

The only value that y can not take is the HA y=0, so the range is R: y in R

`R\colon\mleft\lbrace y\in R\mright|y\\eq0\}`

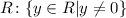
Answer:

VA: x=-3

Holes: x=-2

HA: y=0

Domain: x≠-3, x≠-3

Range: y