We have the expression:
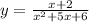
We will start factorizing the denominator:
![\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4\cdot1\cdot6}}{2} \\ x=\frac{-5\pm\sqrt[]{25-24}}{2} \\ x=\frac{-5\pm\sqrt[]{1}}{2} \\ x=(-5\pm1)/(2) \\ x_1=(-5-1)/(2)=-(6)/(2)=-3 \\ x_2=(-5+1)/(2)=-(4)/(2)=-2 \\ \Rightarrow x^2+5x+6=(x+3)(x+2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xjbkjm8bz121984sjbcwwdr11ndyy33soz.png)
Then, we can simplify the expression as:
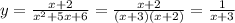
We will have a vertical assymptote at the discontinuity x=-3:
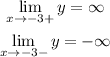
As holes, we can consider x=-2, because in the original equation it would make a discontinuity (it would make zero the quadratic denominator and the numerator), but not an assymptote. The limit exists but the function is not defined for x=-2.
Then, as x=-3 and x=-2 are discontinuities, the domain is D: x in R .
We can calculate if there is an horizontal assymptote calculating the limit of y when x approaches infinity:
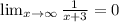
Then, as 0 is a finite value, we have an HA at y=0.
The range is all the values that y can take given the domain.
The only value that y can not take is the HA y=0, so the range is R: y in R
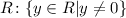
Answer:
VA: x=-3
Holes: x=-2
HA: y=0
Domain: x≠-3, x≠-3
Range: y