Given:
c = total cost.
s = number of songs.
To solve this question, follow the steps below.
Step 01: Find 2 points (s, c).
You can choose 2 points from the table.
Let's choose (14, 8.96) and (16, 10.24).
Step 02: Substitute one point in the general equation.
Given the general equation:
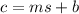
Substituting the first point.
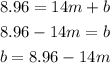
Isolating b by subtracting 8.96 m from both sides:
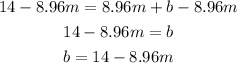
Step 03: Substitute b in the general equation.
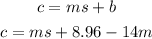
Step 04: Substitute the second point in the equation above.
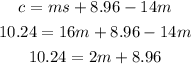
Step 05: Solve the equation above for m.
To do it, first, subtract 8.96 from both sides.
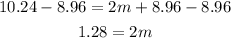
Now, divide both sides by 2.
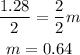
Step 06: Substitute m in the equation from step 02 to find b.
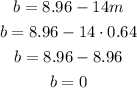
Step 07: Write the equation.
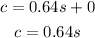
Answer:
c = 0.64s