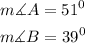Answer:
The measure of Angle A and B are;
Step-by-step explanation:
Given that;
A ls 12° greater than the measure of B;
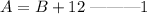
The two angles are complementary;
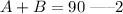
Substituting equation 1 to 2, we have;
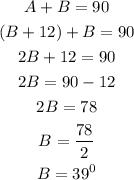
Substituting B into equation 1:
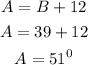
Therefore, the measure of Angle A and B are;