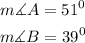Question

The measure of _A ls 12° greater than the measure of_8. The two angles are complementary. Find the measure of each angle. The m_A is and m_Bis le

Answer 1

The measure of Angle A and B are;

`\begin{gathered} m\measuredangle A=51^0 \\ m\measuredangle B=39^0 \end{gathered}`

Step-by-step explanation:

Given that;

A ls 12° greater than the measure of B;

`A=B+12\text{ ---------1}`

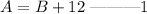
The two angles are complementary;

`A+B=90\text{ -----2}`

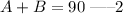
Substituting equation 1 to 2, we have;

`\begin{gathered} A+B=90 \\ (B+12)+B=90 \\ 2B+12=90 \\ 2B=90-12 \\ 2B=78 \\ B=(78)/(2) \\ B=39^0 \end{gathered}`

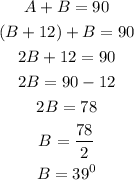
Substituting B into equation 1:

`\begin{gathered} A=B+12 \\ A=39+12 \\ A=51^0 \end{gathered}`

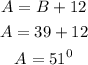
Therefore, the measure of Angle A and B are;

`\begin{gathered} m\measuredangle A=51^0 \\ m\measuredangle B=39^0 \end{gathered}`