Let's look at some logarithm properties,
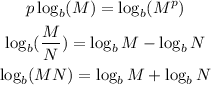
We will use this properties to simplify and write the expression as a single logarithm.
The steps are shown below:
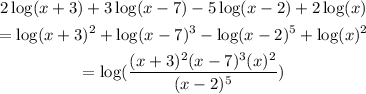
The expression, as a single logarithm, is,
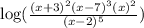
From the answer choices, the correct answer is D.
Answer
D