Question

Rewrite the following expression as a single logarithm: 2log(x+3) + 3log(x - 7) - Slog(x - 2) + 2log(x) 3 log (x+3)(x-7) 12(3-2) 5 A. 5 log (x + 3)?(x - 2) (1-7712 B. 3 (1 +31°160 – 7) log O c. (x-2)-5-1 p2(x+3)*(1-73 log OD. (r-2) 5

Answer 1

Let's look at some logarithm properties,

`\begin{gathered} p\log _b(M)=\log _b(M^p) \\ \log _b((M)/(N))=\log _bM-\log _bN \\ \log _b(MN)=\log _bM+\log _bN \end{gathered}`

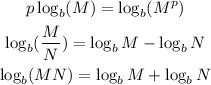
We will use this properties to simplify and write the expression as a single logarithm.

The steps are shown below:

`\begin{gathered} 2\log (x+3)+3\log (x-7)-5\log (x-2)+2\log (x) \\ =\log (x+3)^2+\log (x-7)^3-\log (x-2)^5+\log (x)^2 \\ =\log (((x+3)^2(x-7)^3(x)^2)/((x-2)^5)) \end{gathered}`

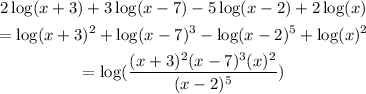
The expression, as a single logarithm, is,

`\log (((x+3)^2(x-7)^3(x)^2)/((x-2)^5))`

From the answer choices, the correct answer is D.

Answer

D