SOLUTION:
Case: Minimum and Maximum functions
Given:

Required: To find the minimum Unit cost
Method: we apply completing square on the function
Step 1: First we find the square of half the coefficient of x
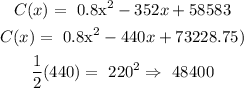
Step 2: Add and subtract the value to the Right Hand Side
![\begin{gathered} C(x)=\text{ 0.8\lparen x}^2-440x+48400-48400+73228.75) \\ Completing\text{ squares in the bracket} \\ C(x)=\text{ 0.8\lbrack\lparen x-220\rparen}^2+24828.75] \\ C(x)=0.8(x-220)^2+\text{ 19863} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v2gr7gzkt27dlsm8v3bcqpgd63l1i724lc.png)
Step 3: From the equation
The quantity need to be produced to get the minimum unit cost is 220.
The value of the minimum cost therefore is obtained at C(220).
This would give:
C(220)= $19863
Final answer:
The minimum unit cost is $19863. Ignore the dollar sign($) when entering your answer.