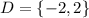Question

Complete Find the intercepts and domain, and perform the symmetry test on each of the following ellipses: (g) 9x^2 + 4y^2 = 16

Answer 1

The intercepts are:

`\begin{gathered} \text{ x-intercept} \\ -2,2 \\ \text{ y-intercept} \\ -3,3 \end{gathered}`

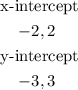
The domain is:

`D=\mleft\lbrace-2,2\mright\rbrace`

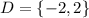
Explanation:

We can calculate the intercepts and the domain as follows:

We must write the equation, in its ellipse form with its center outside the origin

`\begin{gathered} 9x^2\: +\: 4y^2\: =\: 36 \\ \text{The form is:} \\ ((x-h)^2)/(a^2)+\: ((y-k)^2)/(b^2)\: =\: 1 \\ \text{now,} \\ (9)/(36)(x-0)^2\: +\: (4)/(36)(y-0)^2\: =\: (36)/(36) \\ (x^2)/(4)\: +(y^2)/(9)=\: 1 \\ (x^2)/(2^2)\: +\: (y^2\: )/(3^2)=\: 1 \\ a=2 \\ b=3 \end{gathered}`

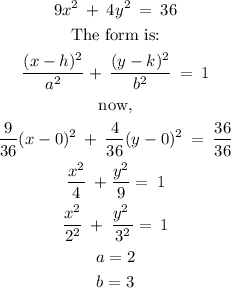
Therefore,

The intercepts are:

`\begin{gathered} \text{ x-intercept} \\ -2,2 \\ \text{ y-intercept} \\ -3,3 \end{gathered}`

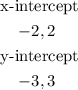
And the domain that are the input values would have the following interval:

`D=\mleft\lbrace-2,2\mright\rbrace`