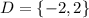ANSWER:
The intercepts are:
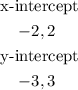
The domain is:
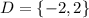
Explanation:
We can calculate the intercepts and the domain as follows:
We must write the equation, in its ellipse form with its center outside the origin
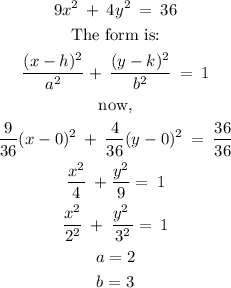
Therefore,
The intercepts are:
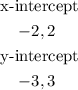
And the domain that are the input values would have the following interval: