Given:
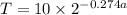
To Determine: The average rate of change of T with respect to a over the interval of 24000 and 30000
Solution
Let us determine the value of a at the interval given
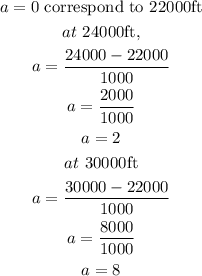
Let us determine the value of T at the given interval using the values of a
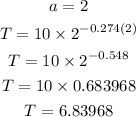
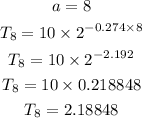
The rate of change would be
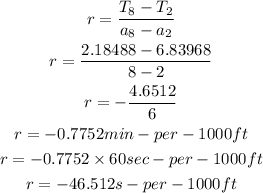
Hence, the rate of change of T with respect to a is -46.512 seconds per 1000ft