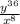ANSWER
y³⁶/x⁸
Step-by-step explanation
To simplify this expression we have to do it from the inner part of the expression to the outer part. First, we have x⁰, which is equal to 1,
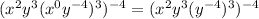
Then we have the interior parenthesis. To simplify this we have to apply the exponent of exponent rule,
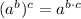
So we have,
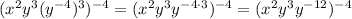
Next, apply the product rule of exponents with the same base,
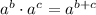
In this case,
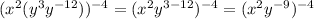
The exponents can be distributed into the multiplication, so we have,
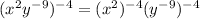
Apply the exponent of exponent rule again,
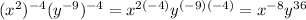
Finally, negative exponents flip the base,
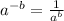
Hence, the simplified expression is,