Question

Which statement are true about the relationship between the functions?

Answer 1

Step 1:

Thus, option 1 is wrong, but option 3 is correct.

Step2:

Now we need to get the vertices of the two graphs

The vertex of a quadratic equation can be gotten using:

`\begin{gathered} -(b)/(2a), \\ Where\text{ the equation is : }ax^2\text{ + bx + c} \\ This\text{ means we need to expand the both equations f and g.} \\ f\text{ = 4(x-}3)^2+6=4(x^2-6x+9)+6 \\ Let\text{ us expand:} \\ f=4x^2\text{ - 24x + 36} \\ \text{Therefore, we can find the vertex of f, where b = -24 and a = 4; this is:} \\ \frac{-\mleft(-24\mright)\text{ }}{2\text{ }*4}_{} \\ \text{vertex of f = 3. (The x value of vertex of f is positive 3)} \\ \text{This means the vertex of f is on the positive side of the x-axis} \\ \text{ } \end{gathered}`

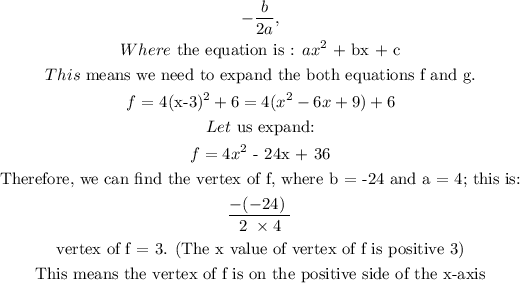
Let us get the y value of the vertex of f as well. We do this by plugging in the value of x at the vertex (i.e. 3) into the equation of f.

`\begin{gathered} y=4(3)^2\text{ - 24(3) + 36 = 0} \\ \text{Thus, at vertex of f, x = 3 and y = 0} \end{gathered}`

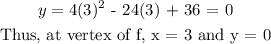
This means that: on the graph of f, y is on the x-axis.

We also need to calculate the value of the vertex of g. We repeat the same process for equation g:

`\begin{gathered} \text{g = -2(x + 1)}^2\text{ + 4} \\ \text{Expand this:} \\ g=-2(x^2\text{ + 2x + 1) + 4} \\ g=-2x^2\text{ -4x - 2 + 4} \\ g=-2x^2\text{ -4x + 2. } \\ In\text{ this equation, a = -2 and b = -4} \\ U\sin g\text{ the formula -b/2a once more to get the vertex of g} \\ \text{vertex of g = }\frac{\text{-(-4)}}{2(2)}\text{ = -1} \\ \text{This means the vertex is on the negative side of the x axis.} \end{gathered}`

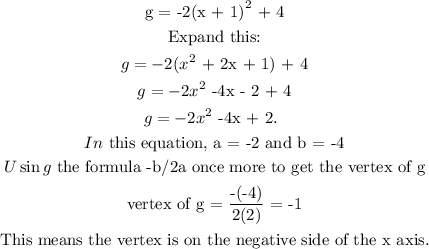
Now to calculate like before, the y-value of g at its vertex.

`\begin{gathered} g=-2x^2\text{ - 4x + 2. Substitute x = -1} \\ y=-2(-1)^2\text{ -4(-1) + 2 = 4} \\ \text{This means the vertex of g has the coordinates: x = -1 and y = 4.} \end{gathered}`

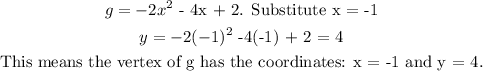
This implies that: In the graph of g, y is 4 units above the x-axis.

We can now calculate the distance between the vertices of both g and f

distance along

For a better understanding, view the diagram below:

The blue graph represents f and the green represents g.

From the diagram, it is easy to compare the vertices of both graphs

Graph of f is 2 units above graph of g ( This implies the last option is correct)

Graph of f is 3 - (-1) = 4 units to the right of g ( this implies the 4th option is correct)

Answers: Options 3, 4, 6