Step 1:
![\begin{gathered} \text{The coefficient of (x-3)}^2\text{ is positive while} \\ \text{The coefficient of (x+1)}^2\text{ is negative.} \\ \text{Therefore, their curves open up in opposite directions} \end{gathered}]()
Thus, option 1 is wrong, but option 3 is correct.
Step2:
Now we need to get the vertices of the two graphs
The vertex of a quadratic equation can be gotten using:
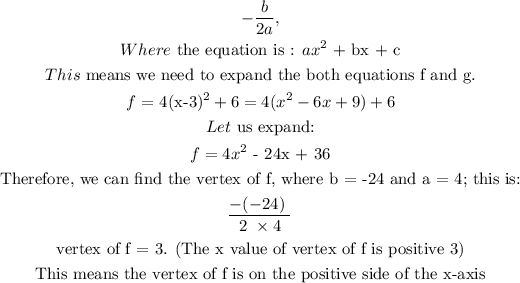
Let us get the y value of the vertex of f as well. We do this by plugging in the value of x at the vertex (i.e. 3) into the equation of f.
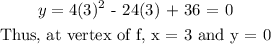
This means that: on the graph of f, y is on the x-axis.
We also need to calculate the value of the vertex of g. We repeat the same process for equation g:
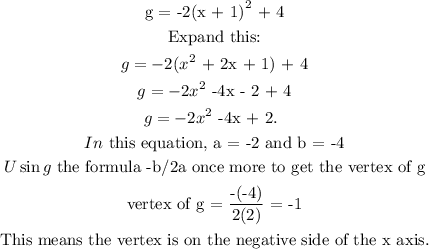
Now to calculate like before, the y-value of g at its vertex.
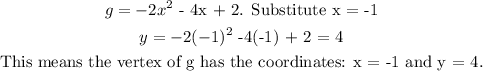
This implies that: In the graph of g, y is 4 units above the x-axis.
We can now calculate the distance between the vertices of both g and f
distance along
For a better understanding, view the diagram below:
The blue graph represents f and the green represents g.
From the diagram, it is easy to compare the vertices of both graphs
Graph of f is 2 units above graph of g ( This implies the last option is correct)
Graph of f is 3 - (-1) = 4 units to the right of g ( this implies the 4th option is correct)
Answers: Options 3, 4, 6