To perform a horizontal translation of a point on the coordinate system you have to add/subtract the constant, k, from the x-coordinate of the point:
• If you add the constant, ,x+k,, the resulting translation will be, k units to the right,.
,
• If you subtract the constant, ,x-k,, the resulting translation will be ,k units to the left,.
To perform a vertical translation of a point on the coordinate system, you have to add/subtract a constant, c, from the y-coordinate of the point.
• If you add the constant, ,y+c,, the resulting translation will be, ,c units up.
,
• If you subtract the constant, ,y-c,, the resulting translation will be, c units down.
The points on the coordinate system were moved 1 unit to the left, which means that you have to subtract 1 unit from the x-coordinate of each point and 7 units up, which means that you have to add 7 units to the y-coordinate of each point.
You can express the translation rule as follows:
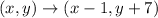

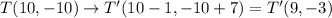
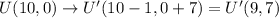
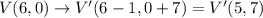
The resulting coordinates after the translation are:
S'(5,-3)
T'(9,-3)
U'(9,7)
V'(5,7)