Answer:
Step-by-step explanation:
The slope-intercept form of the equation of a line is generally given as;

where m = the slope of the line
b = y-intercept of the line
From the given question, we can deduce at day 0, 0 packs of printer paper will be used and at day 60, about 130 packs of paper will be used. We can use this information to determine the slope of the line at (0,0) and (60, 130) using the below formula;
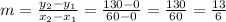
At x = 0, y = 0, therefore the yintercept(b) is 0, which means that the line will start at the origin.
So the equation of the line is given as;
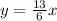
The graph of the line is as shown below;
To determine how many packs of paper will remain after 20 days, all we need to do is set x = 20 and solve for y;
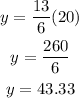
43.33 packs of papers would have been used after 20 days as seen above.
130 - 43.33 = 86.7 packs
So the manager should expect about 86.7 packs to remain after 20 days