All of the given equations have the following general form:
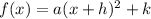
To analyze the equations and find their corresponding graph, we need to remember the following:
• If a>0, the parabola will open upwards, and if a<0, the parabola will open downwards.
,
• The point (-h,k) is the vertex of the parabola.
Let's start with the first function:
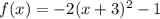
And identify a, h and k:
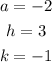
since a<0, the parabola will open downwards (this discards the first and third graphs since they open upwards).
And the vertex of the parabola is at:
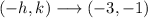
And as we can see, the fourth graph is the one that opens downwards and has its vertex at (-3,-1):
We continue with the second function:
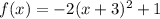
It is very similar to the first option. Since a<0, the parabola opens downwards. And the vertex is at:
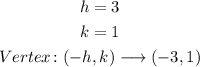
The second graph is the one that meets these characteristics:
Now, we analyze the third function:
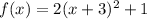
And identify a, h and k:
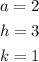
Since a>0, the parabola will open upwards. Now we find the vertex point to decide if this is represented by the first or the third graph:

These characteristics coincide with the first graph:
Finally, we analyze the fourth function:
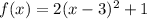
Identify a, h an k:
![undefined]()
Again a>0, thus the parabola will open upwards.