Question

I just need the answer

Answer 1

All of the given equations have the following general form:

`f(x)=a(x+h)^2+k`

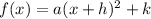
To analyze the equations and find their corresponding graph, we need to remember the following:

• If a>0, the parabola will open upwards, and if a<0, the parabola will open downwards.

,

• The point (-h,k) is the vertex of the parabola.

Let's start with the first function:

`f(x)=-2(x+3)^2-1`

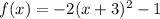
And identify a, h and k:

`\begin{gathered} a=-2 \\ h=3 \\ k=-1 \end{gathered}`

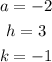
since a<0, the parabola will open downwards (this discards the first and third graphs since they open upwards).

And the vertex of the parabola is at:

`(-h,k)\longrightarrow(-3,-1)`

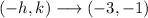
And as we can see, the fourth graph is the one that opens downwards and has its vertex at (-3,-1):

We continue with the second function:

`f(x)=-2(x+3)^2+1`

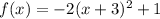
It is very similar to the first option. Since a<0, the parabola opens downwards. And the vertex is at:

`\begin{gathered} h=3 \\ k=1 \\ Vertex\colon(-h,k)\longrightarrow(-3,1) \end{gathered}`

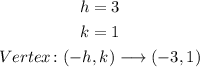
The second graph is the one that meets these characteristics:

Now, we analyze the third function:

`f(x)=2(x+3)^2+1`

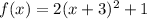
And identify a, h and k:

`\begin{gathered} a=2 \\ h=3 \\ k=1 \end{gathered}`

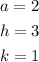
Since a>0, the parabola will open upwards. Now we find the vertex point to decide if this is represented by the first or the third graph:

`(-h,k)\longrightarrow(-3,1)`

These characteristics coincide with the first graph:

Finally, we analyze the fourth function:

`f(x)=2(x-3)^2+1`

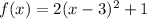
Identify a, h an k:

Again a>0, thus the parabola will open upwards.