Set A contains multiples of 10 from 10 to 90. Set B contains multiples of 30 from 30 to 120. Set C contains even numbers from 2 to 20. Find (A ∪ B) ∩ C.

Question

asked Apr 25, 2023 169k views

1 Answer

Hao Wooi Lim · Answer 1 · 2023-05-01T05:13:11+0000

ANSWER

$(A\cup B)\operatorname{\cap}C=\lbrace10,20\rbrace$

Step-by-step explanation

Set A contains multiples of 10 from 10 to 90:

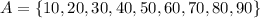
$A=\lbrace10,20,30,40,50,60,70,80,90\rbrace$

Set B contains multiples of 30 from 30 to 120:

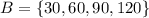
$B=\lbrace30,60,90,120\rbrace$

The union of two sets is the set that contains all the values in both sets. Therefore, A U B is:

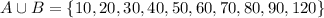
$A\cup B=\lbrace10,20,30,40,50,60,70,80,90,120\rbrace$

Set C contains even numbers from 2 to 20:

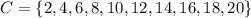
$C=\lbrace2,4,6,8,10,12,14,16,18,20\rbrace$

The intersection of two sets is the set of values that exist in the two sets. Therefore, (A U B) n C is:

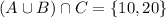
$(A\cup B)\cap C=\lbrace10,20\rbrace$

That is the answer.