Question

How do you find the vertex and the domain and range interval notion

Answer 1

Consider the given quadratic equation,

`y=-4x^2-8x-3`

Since the tangent at the vertex is a perfectly horizontal line, so its slope will be zero.

So we can equate the first derivative of the function to zero, in order to obatin the vertex as,

`\begin{gathered} y^(\prime)=0 \\ (-4x^2-8x-3)^(\prime)=0 \\ -4(2x)-8(1)-0=0 \\ -8x-8=0 \\ -8(x+1)=0 \\ x+1=0 \\ x=-1 \end{gathered}`

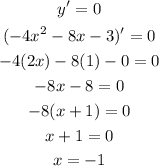
Solve for the corresponding y-coordinate as,

`\begin{gathered} y=-4(-1)^2-8(-1)-3 \\ y=-4+8-3 \\ y=1 \end{gathered}`

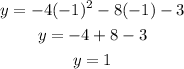
Thus, the vertex of the parabola lies at (-1,1).

Now, let us find the right end of the parabola, which lies at the x-axis. So its y-coordinate will be zero,

`\begin{gathered} -4x^2-8x-3=0 \\ 4x^2+8x+3=0 \\ 4x^2+2x+6x+3=0 \\ 2x(2x+1)+3(2x+1)=0 \\ (2x+1)(2x+3)=0 \\ 2x+1=0\text{ }or\text{ }2x+3=0 \\ x=(-1)/(2)\text{ }or\text{ }x=(-3)/(2) \end{gathered}`

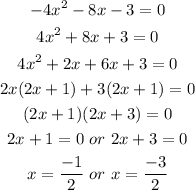
Thus, the parabola intersects the x-axis at points (-1/2, 0) and (-3/2, 0).

The rightmost point of these two will be the other extreme of the parabolic curve.

So the parabola has right end point at x= -1/2.

Also note that it is clearly visible that the left extreme of the parabola is x=-2.

So it can be concluded that the functions spans from x=-2 to x=-1/2.

Therefore, the domain of the function is [-2, -1/2).

The y-coordinate corresponding to x=-2 is calculated as,

`\begin{gathered} y=-4(-2)^2-8(-2)-3 \\ y=-16+16-3 \\ y=-3 \end{gathered}`

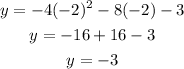
Thus, the lower extreme of the function is y=-3, while the upper extreme lies at the vertex y=1.

Therefore, the range of the function is [-3, 1].