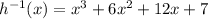Answer:
Step-by-step explanation:
Given the below function;
![h(x)=\sqrt[3]{x+1}-2](https://img.qammunity.org/2023/formulas/mathematics/college/pgsrg0tey6uvcup99kjky8ci4dpgyom697.png)
We'll follow the below steps to determine the inverse of the above function;
Step 1: Replace h(x) with y;
![y=\sqrt[3]{x+1}-2](https://img.qammunity.org/2023/formulas/mathematics/college/gp1meeb7zwfwo8jrda62noq1ldca19zqck.png)
Step 2: Switch x and y;
![x=\sqrt[3]{y+1}-2](https://img.qammunity.org/2023/formulas/mathematics/college/if3krk7jdk7itsjk3gznevy9yuxl71aq8l.png)
Step 3: Solve for y by first adding 2 to both sides;
![\begin{gathered} x+2=\sqrt[3]{y+1}-2+2 \\ x+2=\sqrt[3]{y+1} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sirdt2kk7tk6wr4c6fjc346tz47np66gr6.png)
Step 4: Take the cube of both sides;
![\begin{gathered} (x+2)^3=(\sqrt[3]{y+1})^3 \\ (x+2)^3=y+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ctgopiekg2wwi2bdbz5yllibhxjbduhqaa.png)
Step 5: Expand the cube power;
Recall;
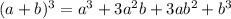
Applying the above, we'll have;
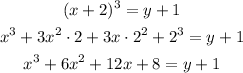
Step 6: Subtract 1 from both sides of the equation;

Step 7: Replace y with h^-1(x);