SOLUTION
The diagram below will help us answer the question
From the diagram above, Area of the shaded region is
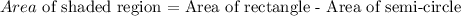
From the diagram, the rectangle has a width of 9 ft, which is also the radius of the semi-circle. So the length of the rectangle is also equal to the diameter of the semi-circle, which is
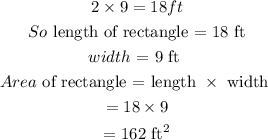
Area of a semi-circle is given as
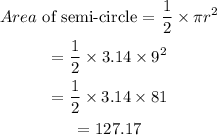
Area of shaded region becomes
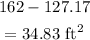
Hence the answer is 34.83 square-feet