Question

The larger of two integers is 4 more than 9 times the smaller. The sum of the two integers is greater than or equal to 26. Find the smaller possible integer values for both of these integers.

Answer 1

We are given 2 statements.

We translate them to algebraic statements.

Let

smaller integer be s, and

larger integer be l

"The larger of two integers is 4 more than 9 times the smaller."

We can write this as:

`l=9s+4`

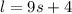
Then, we are given sum of 2 integers is greater than or equal to 26, we can write:

`l+s\geq26`

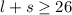
We put 1st equation in 2nd:

`\begin{gathered} l+s\geq26 \\ 9s+4+s\geq26 \\ 10s\geq22 \\ s\geq2.2 \end{gathered}`

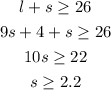
The next integer value (smallest of them all) of s is "3".

Now, if s is 3, l would be:

l = 9s + 4

l = 9(3) + 4

l = 27 + 4

l = 31

smaller of the both integers:

Smaller Number: 3

Larger Number: 31