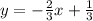ANSWER:
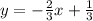
Explanation:
The equation of the line in its slope and intercept form is as follows:
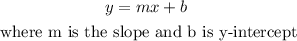
The slope can be calculated as follows:

Replacing the points (-1 , 1) and (5 , -3) :
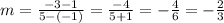
Now, we calculate the value of b, with the help of the slope and the point (-1,1)

Therefore, the equation would be: