Question

Last year, Kaitlyn had $30,000 to invest. She invested some of it in an account that paid 5% simple interest per year, and she invested the rest in an account that paid 9% simple interest per year. After one year, she received a total of $2580 in interest. How much did she invest in each account?First account:Second account:

Answer 1

She invested an amount of $3,000 in the first accont and $27,000 in the second account

Step-by-step explanation:

Here, we want to get the amount invested in each of the accounts

To get this,let us write the simple interest formula

Mathematically, we have this as:

`I\text{ = }(PRT)/(100)`

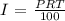
Let the amount invested in the first account be $x, while that of the second account be $y

P represent the amounts invested

R is the rate of investment

T is the time (1 year)

The sum of these two is the $30000 she has to invest

Mathematically, we have this as:

`x\text{ + y = 30000}`

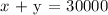
Let us get the interests on each of the accounts

For the first account, we have the interest as:

`I_1\text{ = }(x*5*1)/(100)\text{ = }(5x)/(100)`

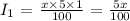
For the second account, we have the interest as:

`I_2\text{ = }(y*9*1)/(100)\text{ =}(9y)/(100)`

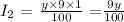
The sum of these two is the interest value, which is as follows:

`\begin{gathered} I_1+I_2\text{ = }(5x)/(100)+(9y)/(100)\text{ = 2580} \\ \\ 5x\text{ + 9y = 258000} \end{gathered}`

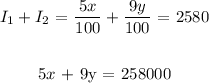
So, we have two equations to solve simultaneously

The two equations are:

`\begin{gathered} x\text{ + y = 30000} \\ 5x\text{ + 9y = 258000} \end{gathered}`

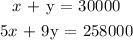
We can solve this by substitution

Let us substitute for y

`y\text{ = 30000-x}`

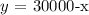
Insert this into the second equation, we have this as:

`\begin{gathered} 5x\text{ + 9(30000-x) = 258000} \\ 5x\text{ + 270000-9x = 258000} \\ 9x-5x\text{ = 270000-258000} \\ 4x\text{ = 12000} \\ x\text{ = }(12000)/(4) \\ x\text{ = 3,000} \end{gathered}`

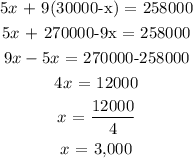
Recall:

`y\text{ = 30000-x = 30000-3000 = 27000}`

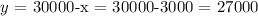
What this mean is that:

She invested an amount of $3,000 in the first accont and $27,000 in the second account