Question

A football player kicks a football off a tee with a speed of 16 m/s at an angle of 63°. How far is the ball from the football player when it lands? How much farther would the ball go if he kicked it with the same speed, but at a 45° angle? Which ball will land first: the ball kicked at 16 m/s and at a 63° angle, or one kicked at 9 m/s and at a 45° angle?

Answer 1

A football player kicks a football off a tee with a speed of 16 m/s at an angle of 63°

The horizontal and vertical speed of the ball is given by

`\begin{gathered} v_x=v\cos (\theta) \\ v_y=v\sin (\theta) \end{gathered}`

Where v = 16 m/s and θ = 63°

`\begin{gathered} v_x=16\cos (63\degree)=7.26\; (m)/(s) \\ v_y=16\sin (63\degree)=14.26\; (m)/(s) \end{gathered}`

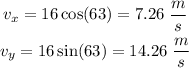
How far is the ball from the football player when it lands?

The range of the ball is given by

`x=v_x* t`

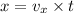
Where t is the time the ball remains in the air.

The time (t) can be found as

`y=v_yt+(1)/(2)at^2`

y = 0 when the ball is in the air.

The acceleration is due to gravity (-9.8 m/s²)

`\begin{gathered} 0=14.26t+(1)/(2)(-9.8)t^2 \\ 0=14.26t-4.9t^2 \\ 0=t(14.26-4.9t) \\ 0=14.26-4.9t \\ 4.9t=14.26 \\ t=(14.26)/(4.9) \\ t=2.91\; s \end{gathered}`

Finally, the range is

`x=v_x* t=7.26*2.91=21.13\; m`

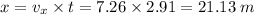
Therefore, the ball will land 21.13 meters far from the football player.

How much farther would the ball go if he kicked it with the same speed, but at a 45° angle?

We need to repeat the above calculations

The horizontal and vertical speed of the ball is given by

`\begin{gathered} v_x=v\cos (\theta)=16\cos (45\degree)=11.31\; (m)/(s) \\ v_y=v\sin (\theta)=16\sin (45\degree)=11.31\; (m)/(s) \end{gathered}`

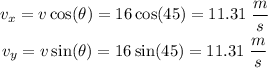
The time (t) is given by

`\begin{gathered} y=v_yt+(1)/(2)at^2 \\ 0=11.31_{}t+(1)/(2)(-9.8)t^2 \\ 0=11.31_{}t-4.9t^2 \\ 0=11.31_{}-4.9t \\ 4.9t=11.31_{} \\ t=\frac{11.31_{}}{4.9} \\ t=2.31\; s \end{gathered}`

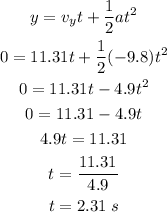
Finally, the range is

`x=v_x* t=11.31*2.31=26.13\; m`

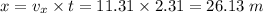
Therefore, the ball will land 26.13 meters far from the football player.

Which ball will land first: the ball kicked at 16 m/s and at a 63° angle, or one kicked at 9 m/s and at a 45° angle?

The ball kicked at 16 m/s and at a 63° angle takes 2.91 s to land.

The ball kicked at 9 m/s and at a 45° angle will take

`v_y=9\sin (45\degree)=6.36\; (m)/(s)`
`\begin{gathered} y=v_yt+(1)/(2)at^2 \\ 0=6.36t+(1)/(2)(-9.8)t^2 \\ 0=6.36t-4.9t^2 \\ 0=6.36-4.9t \\ 4.9t=6.36 \\ t=(6.36)/(4.9) \\ t=1.30\; s \end{gathered}`

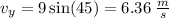
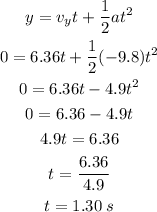
So, the ball kicked at 9 m/s and at a 45° angle takes 1.30 s to land.

Therefore, the ball kicked at 9 m/s and at a 45° angle will land first.