This is a basic permutation and combination problem.
With permutations,
we care about the order of the elements.
With combinations,
we don't care about ordering.
In this problem, we don't really care in the order we select 3 people from 8 person. So, we will use combination. The answer is:
8 C 3.
The combination formula is:
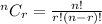
Note: n! is n * (n-1) * (n-2) * ...
Let's calculate 8C3. Shown below:
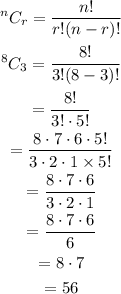
There are 56 different committees possible.