Question

Decide whether each of the following function is even add or neither show or explain your reasoning

Answer 1

To answer this question, we need to remember the following key concept:

• A function is even if we check that,:

`f(-x)=f(x)`

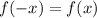
In this case, we can say that the function has been reflected in the y-axis.

• Likewise, we can say that a function is odd if we check that:

`f(-x)=-f(x)`

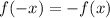
Then, we need to check these two situations with the three given functions as follows:

First case

`f(x)=(2)/(3)x+1`

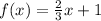
1. We need to check if the function is even:

`f(-x)=(2)/(3)(-x)+1=-(2)/(3)x+1\Rightarrow f(-x)=-(2)/(3)x+1`

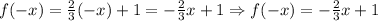
We can check that:

`f(-x)\\e f(x)`
`f(x)=(2)/(3)x+1\\e f(-x)=-(2)/(3)x+1`

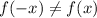
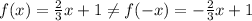
Therefore, the function is not even.

2. We need to verify if the function is odd:

`f(-x)=-f(x)`
`-f(x)=-((2)/(3)x+1)=-(2)/(3)x-1`

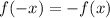
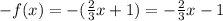
Then, we have:

`f(-x)=-(2)/(3)x+1\\e-f(x)=-(2)/(3)x-1`

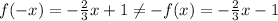
Then, the function is not odd.

Therefore, the function is neither even nor odd.

Second case

We can proceed in a similar way as before:

1. We need to verify if the function is even:

`f(x)=f(-x)`
`f(x)=(x+2)^2=x^2+4x+4`
`f(-x)=(-x)^2+4(-x)+4=x^2-4x+4`

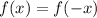
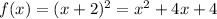
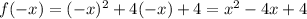
Then

`f(x)\\e f(-x)`

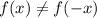
Since

`f(x)=x^2+4x+4\\e f(-x)=x^2-4x+4`

Thus, the function is not even.

2. Verify if the function is odd

`f(-x)=-f(x)`
`-f(x)=-(x^2+4x+4)=-x^2-4x-4`

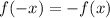
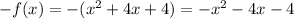
Then, we have that:

`f(-x)\\e-f(x)\Rightarrow f(-x)=x^2-4x+4\\e-x^2-4x-4`

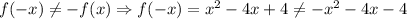
Hence, the function is not odd.

Therefore, the function is neither even nor odd.

Third Case

We have the function:

`f(x)=|x|-x^2`

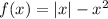
We need to remember that |x| is the function absolute value.

1. Is the function even?

Then, we have:

`f(-x)=|-x|-(-x)^2=|-(-x)|-x^2=|x|-x^2`

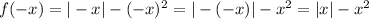
Then, we can see that the function is even, since:

`f(x)=f(-x)\Rightarrow f(x)=|x|-x^2=f(-x)=|x|-x^2`

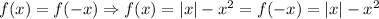
Then, the function is even.

2. Is the function odd?

`-f(x)=-(|x|-x^2)=-|x|+x^2`

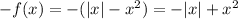
Then, we have:

`f(-x)\\e-f(x)\Rightarrow f(-x)=|x|-x^2\\e-|x|+x^2`

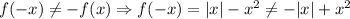
Thus, the function is not odd.

Therefore, this function is even. However, it is not odd.

In summary, we have:

a. The function:

`f(x)=(2)/(3)x+1`

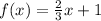
Neither even nor odd.

b. The function:

`f(x)=(x+2)^2`

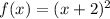
Neither even nor odd.

c. The function:

`f(x)=|x|-x^2`

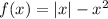
The function is even. However, it is not odd.