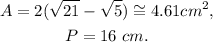Step-by-step explanation
Geometry / Triangles Area and Perimeter
In this problem, we have a diagram of a paper airplane, and we must compute its area and perimeter.
The area of a triangle with height h and base b is:
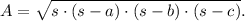
Where:
• a, b and c are the lengths of the sides of the triangle,
,
• s is the semi perimeter, which is given by:
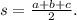
(1) The area of the airplane is given by:
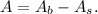
Where:
• Ab is the area of the bigger triangle,
,
• As is the area of the smaller triangle.
Bigger triangle
The bigger triangle has sides a = b = 5 cm and c = 4 cm, is semi perimeter is given by:
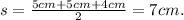
The area of the bigger triangle is:

Smaller triangle
The smaller triangle has sides a = b = 3 cm and c = 4 cm, is semi perimeter is given by:
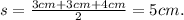
The area of the smaller triangle is:
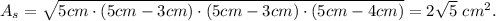
Replacing these results in the formula for the area of the airplane, we get:
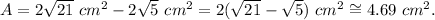
(2) The perimeter of the airplane is the sum of the length of the sides:
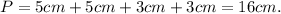
Answer
The area and perimeter of the airplane are: