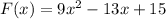Question

Find the particular antiderivative F(x) of f(x) = 18x - 13 that satisfies F(1) = 11.

Answer 1

To get the antiderivative of the function, we will integrate F(x), as follows:

`\begin{gathered} \int (18x-13)dx=\int 18xdx-\int 13dx \\ =(1)/(2)(18x^2)-13x+C \\ =9x^2-13x+C \end{gathered}`

Now, to get the particular antiderivative, we evaluate the antiderivative for x = 1, and it must be equal to 11. This can be shown as:

`\begin{gathered} 9(1)^2-13(1)+C=11 \\ 9-13+C=11 \\ C=11+13-9 \\ C=24-9 \\ C=15 \end{gathered}`

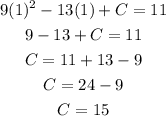
Hence, the particular antiderivative is

`F(x)=9x^2-13x+15`