ANSWER:
52 shrubs
Explanation:
We know the number of trees planted in a given area, so to calculate the number of total trees, we must calculate the area of the entire figure and thus calculate by means of a proportion
We calculate the total area if we divide the figure in two, as follows:
The area of zone A, which is a rectangle, is calculated as follows:

The area of zone B, which is a triangle, is calculated as follows:
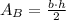
To calculate the value of the height of the triangle, we apply the Pythagorean theorem on the right triangle that is formed:
Where the hypotenuse is 25 meters and the other leg is 15 meters, just like this:
![\begin{gathered} h^2=a^2+b^2 \\ 25^2=15^2+b^2 \\ b=\sqrt[]{25^2-15^2} \\ b=\sqrt[]{400} \\ b=20 \\ \text{therefore the height is 20 meters, replacing:} \\ A_B=(30\cdot20)/(2) \\ A_B=300 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/axeezogenj9tc059rni1nk0dfnobcw5ni1.png)
Now, the total area would be the sum of both areas:
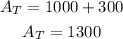
Which means that if in an area of 400 square meters (20 * 20) they can plant 16 shrubs, in an area of 1300 square meters they would be:
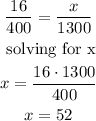
In other words, a total of 52 shrubs can be raised throughout the region.