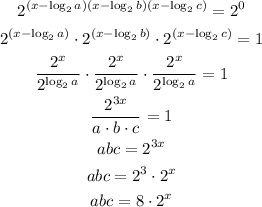We have a fifth degree polynomial:
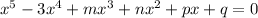
This polinomial has 3 real roots, that can be expressed as: log2(a), log2(b) and log2(c).
Also, it has two imaginary roots, one of which is di (they have to be conjugate, so the other imginary root is -di).
We have to show that abc = 8.
If we consider the information given, we have some information about all the roots.
We can rewrite the polynomial in factorized form as:
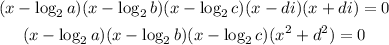
As the polynomial is defined for real numbers, we can write a polynomial with only the real roots as:
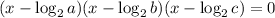
Then, we can relate the roots as: