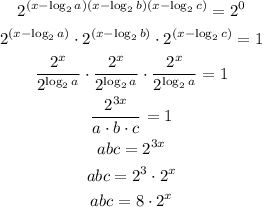Question

Pre calculus 6a. Consider the equation x^5 - 3x^4 + mx^3 + nx^2+ ox + q = 0, where m, n, P, q € R.The equation has three distinct real roots which can be written as log2a, log2b and log2C.The equation also has two imaginary roots, one of which is di where dE R.Show that abc = 8.6b. The values a, b, and C are consecutive terms in a geometric sequence. Show that one of the real roots is equal to 1.6c. Given that q = 8d^2, find the other two real roots.

Answer 1

We have a fifth degree polynomial:

`x^5-3x^4+mx^3+nx^2+px+q=0`

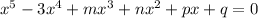
This polinomial has 3 real roots, that can be expressed as: log2(a), log2(b) and log2(c).

Also, it has two imaginary roots, one of which is di (they have to be conjugate, so the other imginary root is -di).

We have to show that abc = 8.

If we consider the information given, we have some information about all the roots.

We can rewrite the polynomial in factorized form as:

`\begin{gathered} (x-\log _2a)(x-\log _2b)(x-\log _2c)(x-di)(x+di)=0 \\ (x-\log _2a)(x-\log _2b)(x-\log _2c)(x^2+d^2)=0 \end{gathered}`

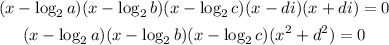
As the polynomial is defined for real numbers, we can write a polynomial with only the real roots as:

`(x-\log _2a)(x-\log _2b)(x-\log _2c)=0`

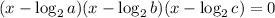
Then, we can relate the roots as:

`\begin{gathered} 2^((x-\log _2a)(x-\log _2b)(x-\log _2c))=2^0 \\ 2^((x-\log _2a))\cdot2^((x-\log _2b))\cdot2^((x-\log _2c))=1 \\ (2^x)/(2^(\log_2a))\cdot(2^x)/(2^(\log_2a))\cdot(2^x)/(2^(\log_2a))=1 \\ (2^(3x))/(a\cdot b\cdot c)^{}=1 \\ abc=2^(3x) \\ abc=2^3\cdot2^x \\ abc=8\cdot2^x \end{gathered}`