Answer:
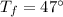
Step-by-step explanation: Two samples of blood that have different masses and temperatures and are mixed, we have to find the final temperature of the mixture. the final temperature can be found using the following formula:
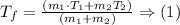
(1) Formula basically tells us that the product of mass and temperature remains constant throughout, so the addition of two products of the two separate blood samples would be equal to the product of final temperature and the total mass of the mixture. Mathematically this means that:
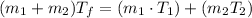
Using (1) and plugging in the corresponding values, we get the answer as follows:
![\begin{gathered} T_f=((m_1\cdot T_1+m_2T_2))/((m_1+m_2))\Rightarrow(1) \\ m_1=6\operatorname{kg} \\ m_2=4\operatorname{kg} \\ T_1=65^(\circ) \\ T_2=20^(\circ) \\ \therefore\rightarrow \\ T_f=\frac{(6kg\cdot65^(\circ)+4\operatorname{kg}\cdot20^(\circ))}{(6kg+4\operatorname{kg})}=((390+80))/(10)=(470)/(10)=47^(\circ) \\ \therefore\rightarrow \\ T_f=47^(\circ) \end{gathered}]()