Answer
The values of a that ensures that the system has at least one solution is
a > (21/127)
Step-by-step explanation
We are told to find the values of a that ensures that the system has at least one solution. The system of equations include
3 (a - 5x) < 1 + x
2 - (x/2) > 3 + 5 (x - a)
To do this, we need to solve the expressions
3 (a - 5x) < 1 + x
3a - 15x < 1 + x
We can rewrite this as
1 + x > 3a - 15x
x + 15x > 3a - 1
16x > 3a - 1
Divide both sides 16
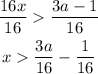
We then solve the second one. But to do this, let's multiply through by 2
2 - (x/2) > 3 + 5 (x - a)
4 - x > 6 + 10 (x - a)
we can rewrite as
6 + 10 (x - a) < 4 - x
6 + 10x - 10a < 4 - x
10x + x < 10a - 6 + 4
11x < 10a - 2
Divide both sides by 11
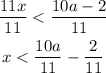
The two solutions are
x > (3a/16) - (1/16)
x < (10a/11) - (2/11)
To find a lasting solution, we need the inequality sign to be the same, so, we need to multiply through one of the equations by -1
x > (3a/16) - (1/16)
-x < (-3a/16) + (1/16)
So, the system of equations become
-x < (-3a/16) + (1/16)
x < (10a/11) - (2/11)
We can then add the two equations
-x + x < (-3a/16) + (1/16) + (10a/11) - (2/11)
0 < (-3a/16) + (10a/11) + (1/16) - (2/11)
0 < -0.1875a + 0.9091a + 0.0625 - 0.1818
0 < 0.7216a - 0.1193
Rewrite
0.7216a - 0.1193 > 0
0.7216a > 0.1193
Divide both sides by 0.7216
(0.7216a/0.7216) > (0.1193/0.7216)
a > 0.1653
a > (21/127)
Hope this Helps!!!