Answer:
t = 42.4 years
Step-by-step explanation:
To find the amount of time needed for the sample to decay, you need to use the half-life equation:
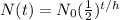
In this equation,
-----> N(t) = final mass (mg)
-----> N₀ = initial mass (mg)
-----> t = time passed (yrs)
-----> h = half-life (yrs)
You can find how much time passed by plugging the given variables into the equation and solving for "t". The final answer should have 3 sig figs like the given values.
N(t) = 9.38 mg t = ? yrs
N₀ = 25.0 mg h = 30.0 yrs
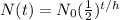 <----- Half-life equation
<----- Half-life equation
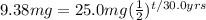 <----- Insert variables
<----- Insert variables
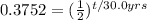 <----- Divide both sides by 25.0 mg
<----- Divide both sides by 25.0 mg
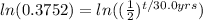 <----- Take the natural log of both sides
<----- Take the natural log of both sides
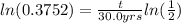 <----- Rearrange the exponent
<----- Rearrange the exponent
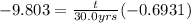 <----- Solve the natural logs
<----- Solve the natural logs
 <----- Divide both sides by -0.6931
<----- Divide both sides by -0.6931
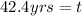 <----- Multiply both sides by 30.0 yrs
<----- Multiply both sides by 30.0 yrs