From the triangle below, if AD = 2 and CD= 8. Length of side AB

Question

asked Jul 2, 2023 232k views

1 Answer

Belegnar · Answer 1 · 2023-07-08T21:06:12+0000

Given: A triangle ABC with a point D on AC such that

$\begin{gathered} AD=\text{ 2 units} \\ CD=8\text{ units} \\ \angle BDC=90\degree \end{gathered}$

Required: To determine the length of side AB.

Step-by-step explanation: In triangle ABC, applying the Pythagoras theorem as

Now,

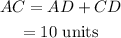
$\begin{gathered} AC=AD+CD \\ =10\text{ units} \end{gathered}$

Thus,

$100=AB^2+BC^2\text{ ...}(1)$

Now, triangle ABD is a right-angled triangle with AB as the hypotenuse. Applying the Pythagoras theorem as-

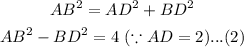
$\begin{gathered} AB^2=AD^2+BD^2 \\ AB^2-BD^2=4\text{ }(\because AD=2)...(2) \end{gathered}$

Similarly, triangle BDC is a right-angled triangle. Thus-

$\begin{gathered} BC^2=BD^2+CD^2 \\ BC^2-BD^2=64\text{ }(\because CD=8)\text{ ...}(3) \end{gathered}$

Subtracting equations (2) and (3) as follows-

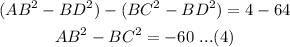
$\begin{gathered} (AB^2-BD^2)-(BC^2-BD^2)=4-64 \\ AB^2-BC^2=-60\text{ }...(4) \end{gathered}$

Again adding equations (1) and (4) as follows-

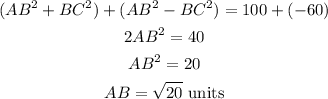
$\begin{gathered} (AB^2+BC^2)+(AB^2-BC^2)=100+(-60) \\ 2AB^2=40 \\ AB^2=20 \\ AB=√(20)\text{ units} \end{gathered}$

Further solving-

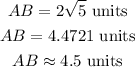
$\begin{gathered} AB=2√(5)\text{ units} \\ AB=4.4721\text{ units} \\ AB\approx4.5\text{ units} \end{gathered}$

Final Answer: Options (a) and (c) are correct.