Given: A triangle ABC with a point D on AC such that
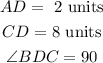
Required: To determine the length of side AB.
Step-by-step explanation: In triangle ABC, applying the Pythagoras theorem as
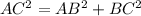
Now,
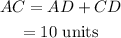
Thus,
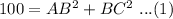
Now, triangle ABD is a right-angled triangle with AB as the hypotenuse. Applying the Pythagoras theorem as-
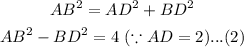
Similarly, triangle BDC is a right-angled triangle. Thus-
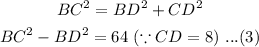
Subtracting equations (2) and (3) as follows-
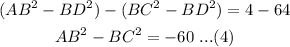
Again adding equations (1) and (4) as follows-
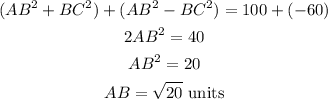
Further solving-
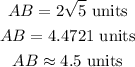
Final Answer: Options (a) and (c) are correct.