For this problem, we are given a function and we need to determine the derivative on the given point.
The function is:

The derivative is:
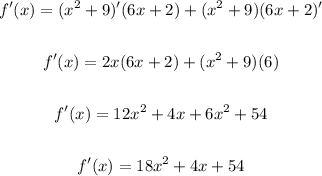
Now we need to apply the given point, which means replacing "x" with 2 and evaluating the expression.
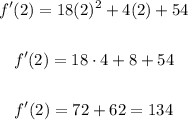
For this problem we used the following differentiation rules: power rule and product rule.