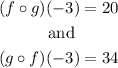1 Answer

Dtjmsy · Answer 1 · 2023-07-20T19:50:30+0000

Given two functions, they can be composed in two ways:

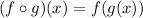
$(f\circ g)(x)=f(g(x))$

It reads "f compound g" or simply "we are going to fill f with g".

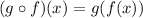
$(g\circ f)(x)=g(f(x))$

It reads "g compound f" or simply "we are going to fill g with f"

So, in this case, you have

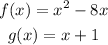
$\begin{gathered} f(x)=x^2-8x \\ g(x)=x+1 \end{gathered}$

Point a.

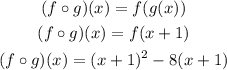
$\begin{gathered} (f\circ g)(x)=f(g(x)) \\ (f\circ g)(x)=f(x+1) \\ (f\circ g)(x)=(x+1)^2-8(x+1) \end{gathered}$

Now, evaluating at -3

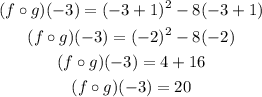
$\begin{gathered} (f\circ g)(-3)=(-3+1)^2-8(-3+1) \\ (f\circ g)(-3)=(-2)^2-8(-2) \\ (f\circ g)(-3)=4+16 \\ (f\circ g)(-3)=20 \end{gathered}$

Point b.

$\begin{gathered} (g\circ f)(x)=g(f(x)) \\ (g\circ f)(x)=g(x^2-8x) \\ (g\circ f)(x)=(x^2-8x)+1 \\ (g\circ f)(x)=x^2-8x+1 \end{gathered}$

Now, evaluating at -3

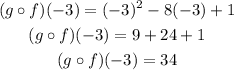
$\begin{gathered} (g\circ f)(-3)=(-3)^2-8(-3)+1 \\ (g\circ f)(-3)=9+24+1 \\ (g\circ f)(-3)=34 \end{gathered}$

Therefore,

$\begin{gathered} (f\circ g)(-3)=20 \\ \text{ and} \\ (g\circ f)(-3)=34 \end{gathered}$

Please log in or register to add a comment.