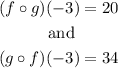Given two functions, they can be composed in two ways:
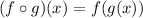
It reads "f compound g" or simply "we are going to fill f with g".
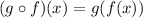
It reads "g compound f" or simply "we are going to fill g with f"
So, in this case, you have
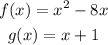
Point a.
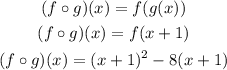
Now, evaluating at -3
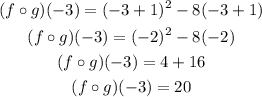
Point b.
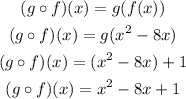
Now, evaluating at -3
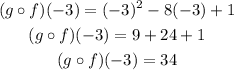
Therefore,